1. Matriks
Matriks adalah kumpulan bilangan atau unsur yang disusun menurut baris dan kolom. Bilangan-bilangan yang disusun tersebut disebut elemen-elemen atau komponen-komponen matriks. Nama sebuah matriks dinyatakan dengan huruf kapital. Banyak baris x banyak suatu kolom dari suatu matriks disebut ordo matriks.
Secara umum matriks dapat ditulis dengan :
Dalam hal ini aij disebut elemen matriks pada baris ke-i dan kolom ke-j.
2. Beberapa Jenis Matriks
(i) Matriks Nol (0)
Adalah matriks yang semua elemennya bernilai nol.
Adalah matriks yang semua elemennya bernilai nol.
(ii) Matriks bujur sangkar
Adalah matriks yang banyak barisnya sama dengan banyak kolomnya.
(iii) Matriks Bujur sangkar
Adalah matriks yang banyak barisnya sama dengan banyak kolomnya.
(iv) Matriks Diagonal
Adalah matriks bujur sangkar yang semua elemen diluar elemen diagonal utama bernilai nol.

(v) Matriks Identitas
Adalah matriks skalar yang elemen-elemen pada diagonal utamanya bernilai satu.

(vi) Matriks Segitiga Atas
Adalah matriks bujur sangkar yang elemen-elemen dibawah diagonal utamanya bernilai nol.

(vii) Matriks Segitiga Bawah
Adalah Matriks bujur sangkar yang elemen-elemen diatas diagonal utamanya bernilai nol.

3. Operasi Matriks


4. Transpos Matriks
Transpos dari suatu matriks merupakan pengubahan baris menjadi kolom dan kolom menjadi baris. Tranpos dari matriks A dinotasikan dengan AT atau At.

Sifat : (AT) T = A
5. Determinan Matriks
Matriks yang mempunyai determinan hanyalah matriks bujur sangkar (banyaknya baris sama dengan banyaknya kolom).

Sifat-sifat determinan matriks:

6. Invers matriks
Bila maka invers dari A adalah :
maka invers dari A adalah :

Syarat ad-bc 0
0

(v) Matriks Identitas
Adalah matriks skalar yang elemen-elemen pada diagonal utamanya bernilai satu.

(vi) Matriks Segitiga Atas
Adalah matriks bujur sangkar yang elemen-elemen dibawah diagonal utamanya bernilai nol.

(vii) Matriks Segitiga Bawah
Adalah Matriks bujur sangkar yang elemen-elemen diatas diagonal utamanya bernilai nol.

3. Operasi Matriks
- Penjumlahan atau pengurangan matriks
Matriks A dan B dapat dijumlahkan atau dikurangkan jika ordo A = ordo B

b. Perkalian Matriks dengan Skalar Jika Skalar dikalikan dengan matriks, maka akan diperoleh sebuah matriks yang elemen- elemennya merupakan perkalian skalar tersebut dengan setiap elemen matriks.


Sifat-sifat:

c. Perkalian Dua Matriks
Dua matriks A dan B dapat dikalikan bila banyak kolom matriks pertama (kiri) sama dengan banyak baris matriks kedua (kanan).
Jika diketahui Matriks Amxn dan Bnxk maka : 

Sifat-sifat:

c. Perkalian Dua Matriks
Dua matriks A dan B dapat dikalikan bila banyak kolom matriks pertama (kiri) sama dengan banyak baris matriks kedua (kanan).


4. Transpos Matriks
Transpos dari suatu matriks merupakan pengubahan baris menjadi kolom dan kolom menjadi baris. Tranpos dari matriks A dinotasikan dengan AT atau At.

Sifat : (AT) T = A
5. Determinan Matriks
Matriks yang mempunyai determinan hanyalah matriks bujur sangkar (banyaknya baris sama dengan banyaknya kolom).


Sifat-sifat determinan matriks:

6. Invers matriks
Bila
 maka invers dari A adalah :
maka invers dari A adalah :
Syarat ad-bc
 0
0
Jawab:
Sifat-sifat :
VEKTOR
1. Pengertian vektor
Pada garis berarah dari titik A ke titik B di R 3 mempunyai panjang tertentu dinyatakan sebagai vektor. Vektor dapat dinotasikan dengan :
2. Panjang Vektor
Jika titik A (x1,y1,z1) dan B (x2,y2,z2) maka vektor AB adalah :
3. Vektor Satuan
4. Operasi Penjumlahan, Pengurangan dan Perkalian Vektor dangan Skalar
a. Penjumlahan atau pengurangan vektor
Contoh :
Jawab :
b. Perkalian Skalar dengan vektor
5. Rumus Perbandingan, Perkalian Skalar Proyeksi dan Perkalian Silang Vektor
a. Perkalian Skalar
b. Cross Product
d. Rumus Pembagian
Jawab :
PERSAMAAN LINGKARAN
Persamaan Lingkaran Garis Singgung
A. Persamaan Lingkaran yang berpusat di O (0, 0) dan berjari-jari r.
Dari gambar, diperoleh persamaan : OP = r
Sehingga diperoleh persamaan lingkaran dengan pusat di O dan berjari-jari r , yaitu :
B. Persamaan Lingkaran yang berpusat di P (a, b) dan berjari-jari r.
Gambar di atas adalah sebuah lingkaran dengan pusat (a, b) dan berjari-jari r. Titik Q (x, y) adalah sebuah titik pada lingkaran.
Dari gambar diperoleh persamaan : PQ = r
C. Persamaan Umum Lingkaran
Bila kita menjabarkan persamaan :
Dan mengatur kembali suku-sukunya, maka akan diperoleh :
Dengan :
D. Persamaan garis singgung lingkaran
1. Garis singgung lingkaran melalui sebuah titik lingkaran
2. Garis singgung dengan gradien yang diketahui.
Langkah menentukan gradien ( m ) untuk persamaan (10) adalah sebagai berikut :
2. Dengan mengambil nilai D=0 , maka dipetoleh nilai m.
LOGARITMA
Logaritma merupakan fungsi invers dari eksponen.
Dengan a = bilangan pokok ,  yang merupakan invers (cerminan dari f(x) terhadap garis y = b) dari fungsi eksponen
yang merupakan invers (cerminan dari f(x) terhadap garis y = b) dari fungsi eksponen  , sehingga
, sehingga  mempunyai invers
mempunyai invers  .
.
 yang merupakan invers (cerminan dari f(x) terhadap garis y = b) dari fungsi eksponen
yang merupakan invers (cerminan dari f(x) terhadap garis y = b) dari fungsi eksponen  , sehingga
, sehingga  mempunyai invers
mempunyai invers  .
.
I. Sifat-sifat Logaritma
a. Sifat Perkalian Logaritma
Perkalian logaritma samadengan penjumlahan logaritma dengan basis tetap.
b.Sifat Pembagian Logaritma
Jika hasil logaritma merupakan pembagian,hasilnya dapat diuraikan menjadi operasi pengurangan bilangan logaritma dengan basis tetap.
c. Sifat Perpangkatan Logaritma
Hasil operasi berupa bilangan logaritma berpangkat, dapat diuraikan sbb:

d. Sifat Penarikan Akar
Jika ada hasil operasi logaritma yang berbentuk akar, ubahlah terlebih dahulu menjadi bentuk pangkat untuk mempermudah penyelesaianya.
Beberapa Sifat Logaritma yang lain:
II. Persamaan Logaritma
III. Pertidaksamaan Logaritma
STATISTIK
A. Ukuran Pemusatan Data
1. Rataan Hitung (Mean)
Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebut mean.
a) Rataan Hitung dari Data Tunggal
b) Rataan Hitung Untuk Data yang Disajikan Dalam Distribusi Frekuensi
Dengan : fixi = frekuensi untuk nilai xi yang bersesuaian
xi = data ke-i
c) Rataan Hitung Gabungan
2. Modus
a. Data yang belum dikelompokkan
Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus dilambangkan mo .
b. Data yang telah dikelompokkan
Modus dari data yang telah dikelompokkan dihitung dengan rumus:
Dengan : Mo = Modus
L = Tepi bawah kelas yang memiliki frekuensi tertinggi (kelas modus) i = Interval kelas
b1 = Frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sebelumnya
b2 = frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sesudahnya
3. Median (Nilai Tengah)
a) Data yang belum dikelompokkan
Untuk mencari median, data harus dikelompookan terlebih dahulu dari yang terkecil sampai yang terbesar.
b) Data yang Dikelompokkan
Dengan : Qj = Kuartil ke-j
j = 1, 2, 3
i = Interval kelas
Lj = Tepi bawah kelas Qj
fk = Frekuensi kumulatif sebelum kelas Qj
f = Frekuensi kelas Qj
n = Banyak data
4. Jangkauan ( J )
Selisih antara nilai data terbesar dengan nilai data terkecil.
5. Simpangan Quartil (Qd)
6. Simpangan baku ( S )
7. Simpangan rata – rata (SR)
8. Ragam (R)
Contoh soal
Tabel 1.1 dibawah ini:
Jawab :








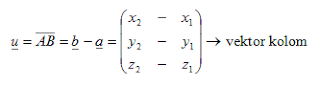





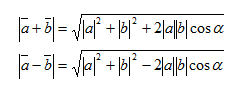















































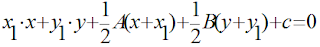































0 comments:
Post a Comment