0 Materi SMA : Fungsi Komposisi dan Invers Pengertian Fungsi Komposisi

Posted by Blogger Name. Category: 1 SMA/IPA , UN Matematika

Fungsi Komposisi dan Invers : Pengertian Fungsi Komposisi

Fungsi komposisi dan invers – Jika terdapat dua buah  fungsi misalkan f  (x) dan g  (x) maka dapat dibentuk fungsi baru dengan menggunakan prinsip operasi komposisi. Operasi komposisi ditulis dengan notasi atau lambang  ○ ( dibaca : komposisi atau bundaran). Fungsi baru yang diperoleh dibentuk dari operasi komposisi fungsi, yaitu:

(i) ( f ○ g ) ( x ), dibaca : f komposisi g x atau f g x

(ii) ( g ○ f ) ( x ), dibaca : g komposisi f x atau g f x.

Perhatikan gambar dibawah ini:

Diagram panah fungsi komposisi dan invers

Dari gambar diatas fungsi g : A ⟶ B. Tiap x ℰ A dipetakan ke y ℰ B, sehingga g : x ⟶ y ditentukan dengan rumus:   y = g ( x ) .

Fungsi f : B ⟶ C. Tiap y ℰ B dipetakan ke z ℰ C, sehingga f : y ⟶ z

ditulis dengan rumus z = f ( y ) .

Fungsi h : A ⟶ C. Tiap x ℰ A dipetakan ke z ℰ C, sehingga h : x ⟶ z

ditulis dengan rumus z = h ( x ).

Fungsi h adalah pemetaan langsung dari himpunan A ke himpunan C. Fungsi h seperti ini disebut komposisi dari fungsi f dan fungsi g , ditulis dengan notasi :  h = f ○ g atau

h ( x ) = ( f ○ g ) ( x ).                                                              © fungsi komposisi dan invers©

Dari uraian fungsi komposisi dan invers diatas , rumus fungsi komposisi f dan g adalah:

Dan rumus fungsi komposisi g dan f adalah:

Agar lebih memahami dan terampil menggunakan rumus fungsi komposisi serta fungsi komposisi dan invers, perhatikan contoh-contoh dibawah ini:

Contoh 1 :

Diketahui f ( x ) = 4 x – 1 dan g ( x ) = x² + 2. Tentukanlah :

(a) ( f ○ g ) ( x )

(b) ( g ○ f ) ( x )

(c) ( f ○ g ) ( -2 )

[Penyelesaian]

(a) ( f ○ g ) ( x ) = f ( g(x) ) = f ( x² + 2 ) = 4 ( x² + 2 ) – 1 =  4 x² + 7

(b) ( g ○ f ) ( x ) = g ( f(x) ) = g (4 x – 1 ) =  ( 4x – 1 )² + 2 = 16x² – 8 x + 3

(c)  ( f ○ g ) ( -2 ) =  4 (-2)² + 7 = 23.

Fungsi komposisi dan invers ,Contoh 2 :

Tentukanlah ( f ○ g  ○ h ) ( x ) jika diketahui f ( x ) = 3 x – 2 , g ( x ) = 4 – x  dan

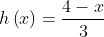
[Penyelesaian]

Bentuk ( f ○ g  ○ h ) ( x ) = ( f ○ g ) ○ h, karena ada tiga fungsi yaitu f , g dan h maka kita tentukan terlebih dahulu ( f ○ g ),

                     

Barulah tentukan ( f ○ g ) ○ h, yaitu,

 

Jadi, ( f ○ g  ○ h ) ( x ) = x + 6.                        

Fungsi komposisi dan invers - Syarat fungsi komposisi

Berkenaan dengan fungsi komposisi dan invers , tidak semua fungsi dapat di komposisikan ada syarat-syarat tertentu yang harus dipenuhi oleh dua fungsi yang akan dikomposisikan. Perhatikan syarat-syarat fungsi komposisi dibawah ini.

(1) Syarat agar fungsi f dan fungsi g dapat di komposisikan menjadi fungsi komposisi

( f ○ g ) adalah irisan antara domain fungsi f dengan range fungsi g bukan himpunan kosong atau 

(2) Domain ( f ○ g ) merupakan himpunan bagian dari domain fungsi g, atau

(3) Range fungsi komposisi ( f ○ g ) merupakan himpunan bagian dari range fungsi f, atauR

Ketiga syarat diatas haruslah benar-benar diperhatikan untuk memahami fungsi komposisi dan invers lebih lanjut.

Contoh 3 :

Diketahui f ( x ) = 2 x – 1 dan g ( x ) = x²  - 1, tentukanlah nilai  a  agar ( g○f○f ) (a) =  - 1

[Penyelesaian]

 

Tentukan terlebih dahulu ( g○f )(x) ,

 

 

Fungsi komposisi dan Invers : Menentukan fungsi jika komposisi dan fungsi yang lain sudah diketahui

Jika fungsi komposisi ( f ○ g ) atau ( g ○ f ) sudah terlebih dahulu diketahui maka fungsi f dan fungsi g dapat ditentukan. Coba perhatikan beberapa contoh soal fungsi komposisi dan invers dibawah ini :

Contoh 4 :

Diketahui ( f ○ g )(x) = x , tentukan nilai g (x) jika,

 

[Penyelesaian]

 

 

fungsi komposisi dan invers,

Contoh 5  :

Diketahui g ( x ) = 4x² – 2, tentukan nilai f ( 2x + 1 )  jika ( g ○ f ) (x) = 16x² + 16x + 2

[Penyelesaian]

↔ ( g ○ f ) (x) = 16x² + 16x + 2

↔ g (f(x)) = 16x² + 16x + 2

↔ 4 f²(x) – 2 = 16x² + 16x + 2

↔  f²(x) = 4x² + 4x + 1 = ( 2x + 1 )²

↔ f (x) = 2x + 1

Jadi, f ( 2x + 1 ) = 2 (2x+1) +1 = 4x +3

Soal-soal tentang fungsi komposisi dan invers banyak sekali ragam dan variasinya, tetapi bagaimanapun bentuk variasi soal tersebut dengan tetap berpegang pada prinsip-prinsip dasarnya tentu saja akan menjadi lebih mudah.

Fungsi Komposisi dan Invers -- Sifat sifat fungsi komposisi

Beberapa sifat fungsi komposisi yang penting, yaitu :

(1) ( f ○ g )(x) ≠ ( g ○ f )(x), operasi komposisi pada fungsi tidak berlaku sifat komutatif

(2) ( f ○ (g○h )(x) = ( (f ○ g)○h )(x), operasi komposisi berlaku sifat asosiatif

(3) ( f ○ I )(x) = ( I ○ f )(x) = f ( x ), I (x) adalah unsur identitas.

Selamat berlatih dan semoga anda terampil menyelesaikan soal-soal yang berhubungan dengan fungsi komposisi dan invers.

sumber

Tweet

Komentar →