Soal No. 1
Perhatikan gambar susunan beberapa hambatan listrik berikut ini! Tentukan hambatan pengganti (hambatan total) antara titik A dan B dari gambar rangkaian di atas!

Perhatikan gambar susunan beberapa hambatan listrik berikut ini! Tentukan hambatan pengganti (hambatan total) antara titik A dan B dari gambar rangkaian di atas!
Pembahasan
Rangkaian di atas adalah rangkaian seri murni, sehingga tinggal dijumlahkan saja.
Rp = 2 + 3 + 6 = 11 Ohm
Soal No. 2
Perhatikan gambar susunan tiga hambatan berikut ini!
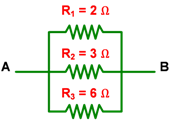
Tentukan hambatan pengganti (hambatan total) antara titik A dan B dari gambar rangkaian di atas!
Pembahasan
Rangkaian di atas berupa paralel murni sehingga :
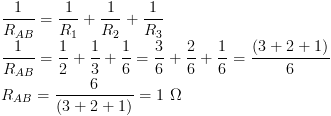
Soal No. 3
10 buah hambatan identik masing-masing sebesar 10 Ω disusun seperti gambar berikut!

Tentukan hambatan pengganti (hambatan total) antara titik A dan B dari gambar rangkaian di atas!
Pembahasan
Seri antara R2 dan R3 , namakan R23 :

Seri antara R4, R5 dan R6 namakan R46 :
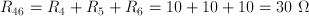
Seri antara R7 , R8 , R9 dan R10 namakan R710

Paralel antara R1, R23, R46 dan R710 menghasilkan RAB:
1/RAB = 1/10 + 1/20 + 1/30 + 1/40
1/RAB = 12/120 + 6/120 + 4/120 + 3/120
RAB = 120 / 25 = 4,8 Ohm
Soal No. 4
10 buah hambatan listrik disusun seperti gambar berikut! Masing-masing hambatan adalah identik dan besarnya 120 Ω .
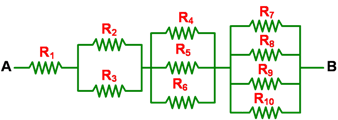
Tentukan hambatan pengganti (hambatan total) antara titik A dan B dari gambar rangkaiandi atas!
Pembahasan
Paralel antara R2 dan R3 namakan R23 sebesar 60 Ω
Paralel antara R4 , R5 dan R6 namakan R46 sebesar 40 Ω
Paralel antara R7 , R8 , R9 dan R10 namakan R710 sebesar 30 Ω
Seri antara R1 , R23 , R46 dan R710 menghasilkan RAB
RAB = 120 + 60 + 40 + 30 = 250 Ω
Soal No. 5
8 buah hambatan dengan nilai masing masing :
R1 = 10 Ω
R2 = 2 Ω
R3 = 3 Ω
R4 = 17 Ω
R5 = 20 Ω
R6 = 20 Ω
R7 = 8 Ω
R8 = 10 Ω

Tentukan hambatan pengganti (hambatan total) antara titik A dan B dari gambar rangkaian di atas!
Pembahasan
→ Seri R3 dan R4 namakan R34
R34 = R3 + R4 = 3 + 17 = 20 Ω
→ Paralel antara R5 dan R34 namakan R35
R35 = 10 Ω
→ Seri antara R2, R35 dan R7 namakan R27
R27 = 2 + 10 + 8 = 20 Ω
→ Paralel antara R27 dan R6 namakan R276
R276 = 10 Ω
→ Seri antara R1 , R276 dan R8 menghasilkan RAB
RAB = 10 + 10 + 10 = 30 Ω
Soal No. 6
8 buah hambatan indentik masing-masing senilai 10 Ω disusun seperti gambar berikut!
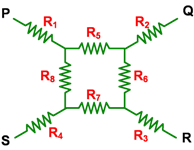
Tentukan hambatan pengganti (hambatan total) antara titik P dan R !
Pembahasan
Karena R2 dan R4 tidak akan di aliri arus listrik / rangkaian terbuka, maka anggap tidak ada.
→ Seri R5 dan R6 :
R56 = 20 Ω
→ Seri R7 dan R8 :
R78 = 20 Ω
→ Paralel R56 dan R78 :
R58 = 10 Ω
→ Seri R1 , R58 dan R3 menghasilkan RPQ :
RPQ = 10 + 10 + 10 = 30 Ω
Soal 7
Diberikan rangkaian seperti gambar dibawah.
Jika R1 = 50 Ω, R2 = 60 Ω, R3 = 40 Ω, R4 = 20 Ω, R5 = 30 Ω

Hitung hambatan pengganti dari rangkaian diatas!
Pembahasan
Pada rangkaian diatas kondisinya adalah:
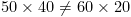
sehingga R5 tidak bisa dihilangkan begitu saja, harus dimasukkan dalam perhitungan. Solusinya adalah mengganti R1, R4 dan R5 dengan 3 buah hambatan baru sebutlah Ra, Rb dan Rc agar rangkaian diatas bisa diselesaikan secara seri / paralel. Berikut ilustrasi dan rumus transformasinya:

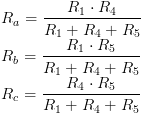
sehingga rangkaian yang baru adalah seperti gambar berikut:

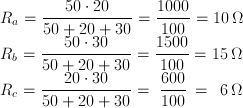
Langkah berikutnya adalah
seri antara Rb dan R2 didapat : 15 + 60 = 75 Ω
seri antara Rc dan R3 didapat : 6 + 40 = 46 Ω
paralel antara dua hasil diatas

terakhir serikan Rparalel dengan Ra sebagai Rtotal :

Dengan demikian didapatkan hambatan pengganti untuk rangkaian jembatan Wheatstone diatas adalah 37,89 Ω.
Soal 8
Berapa nilai kuat arus yang mengalir masuk ke rangkaian listrik berikut ini, jika semua hambatan memiliki nilai yang sama yaitu 12 Ohm dan dipasang sumber tegangan 12 volt?

Pembahasan:
Terlebih dahulu cari hambatan pengganti rangkaian diatas, gunakan rumus berikut:
dengan demikian hambatan total rangkaian adalah
Sehingga nilai kuat arus rangkaian dengan mudah didapat
Soal 9
Perhatikan Gambar dibawah!

Misalkan nilai R1 =6 Ω, R2 = 4 Ω, R3 = 2 Ω, R4 =3 Ω dan R5 =9 Ω.
Berapakah nilai hambatan pengganti rangkaian diatas?
Pembahasan
Jika:
maka R5 dianggap tidak ada atau dihilangkan saja karena tidak akan ada arus listrik yang mengalir melalui R5. Pada soal diatas 6 x 2 = 4 x 3 sehingga ketentuan diatas boleh dipakai. Serikan dua hambatan cabang atas, serikan hambatan cabang bawah kemudian paralelkan hasil keduanya. Hasil yang didapat adalah:
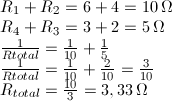



0 comments:
Post a Comment